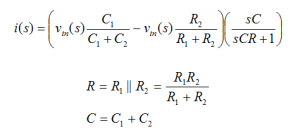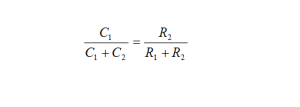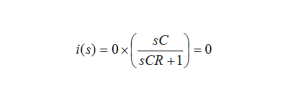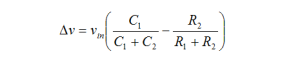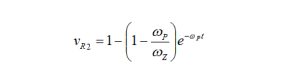I think it was Solomon who said “There is nothing new under the sun.”  You may not remember Solomon, but he is the guy who wrote the lyrics to that song by “The Byrds,” “Turn Turn Turn.”  Essentially, what Solomon said was that all new ideas are just old ones that have been re-entered into the race.

In the late 70s, in a quest to put electronic filters on integrated circuits, the genius’s at Berkeley (and elsewhere) developed the concept of the switched-capacitor filter.  The idea goes something like this—you design an active filter using resistors and capacitors and then replace the resistors with a capacitor and a couple of switches so that it mimics the function of the resistor.  Consider, for example, the damped integrator illustrated in BarNapkin 1.

If you want a switched-capacitor implementation of the damped integrator, you substitute a switched-capacitor equivalent for each resistor. A switched-capacitor equivalent resistor is illustrated in BarNapkin 2.

As shown, all you need is a couple of switches and a capacitor. Of course, you need to drive the switches with the appropriate clocks—it won’t work without them.  Once you do the substitution, you get the circuit shown in BarNapkin 3.

How is it that a capacitor and a couple of switches (driven by non-overlapping clocks) can act like a resistor?  It is pretty simple really.  Consider again, BarNapkin 2.  When the switch on the left is turned on (while the one on the right is off), the capacitor is filled with charge (C times V_in).  Then, when the left switch opens and the right switch turns on, the charge is dumped out of the capacitor.  The time elapsed while the charge was transferred from the input to ground is simply the period of the clock, T.  So the current that flows (on average) is CV_in/T.  Our intuition should be satisfied if we recall that current is charge per unit time (i.e., coulombs per second).  If instead we were to calculate the current through a resistor, we would have found it to be V_in/R.  So, it looks like the capacitor and switches mimic a resistor of value T/C!  The benefits of this little bit of trickery are enormous because it allows integrated circuit designers to build filters whose accuracy depends primarily on the accuracy of clocks and capacitor ratios.  Clocks can be made really accurate—in the ppm range.  What about capacitor ratios?

Once those Berkeley guys (and others) developed the switched-capacitor concept, they went on to figure out how to make perfect capacitor ratios.  Careers were made doing this stuff, and a few Ph.D.s to boot.  After a lot of analyzing and pondering (and dissertating) they came up with some basic principals that you must apply to achieve the best possible capacitor matching.  These are, 1) build all capacitors from multiples of the same unit capacitor (the unit matching principle), 2) lay out capacitors with a common centroid, 3) maximize area to perimeter ratio of the capacitor layout, and 4) match the proximity of all capacitors.  If you follow these rules when you build switched-capacitor filters, you can make very robust high-performance switched-capacitor circuits.

What does all of this have to do with Solomon?  Well, for one thing, the idea of emulating a resistor by switching a capacitor did not originate in the 70’s at Berkeley and elsewhere.  In fact, James Clerk Maxwell had the idea in the previous century.  Who knows, someone may have thought of it before him but did not write it down.  As for those matching principles…?

When I first moved to Austin, Texas in 1980, my buddy and I would frequent “electronic garage sales” in the area.  We would buy things we never used (though we always thought we would).  One of the things I picked up was a Twin-T filter mounted in a metal case with pins on the bottom that fit the footprint of a vacuum tube.  Some years later, I took the thing apart to see what was inside (used to drive my parents crazy when I was a kid!).  What did I find inside but a very old demonstration of the unit-matching principle!  Take a look at the circuit shown in BarNapkin 4.

As you can see, the circuit is made up of integer units of Rs and Cs.  Now look at the pictures showing the Twin-T.  If you look carefully at the components you will count four capacitors and four resistors.  That is what you would expect.  When you make R/2, out of two Rs in parallel, and make the 2C capacitor, out of two Cs in parallel you account for two Rs and two Cs. The other two Rs and Cs are obvious from the schematic.  With further close examination, you see a little disc capacitor.  It is about 22 pF whereas the other capacitors are 7 nF.  I suppose it is there to tweak the notch—even the unit matching principle is not perfect!

Like the switched-capacitor filter and the unit matching principle, I imagine there are other examples of older concepts reapplied in a modern context.  So, I think we can trust Solomon’s wisdom, “There is nothing new under the sun.”

Over the years, a lot of things have changed in the lab.  VOMs have given way to the DMM, analog spectrum analyzers have been replaced by FFT engines, analog storage oscilloscopes have yielded to digital storage scopes—in fact analog scopes sans storage have been virtually replaced by digital ones (my Tek 465 is the mainstay in my lab at home).  And finally, knobs have been punched out by arrays of buttons!  Yet the 10X scope probe has remained fairly constant through the many other technological advances.  Scope probes are interesting.

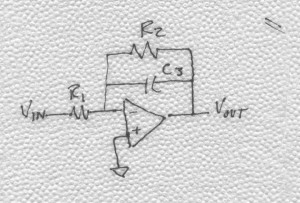
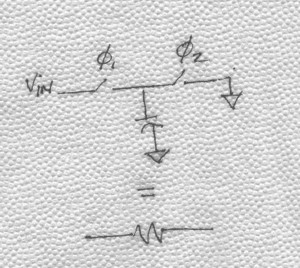
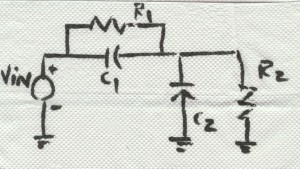
A simplified drawing of a scope-probe network is illustrated in BarNapkin 1.

By observation, you can see that the network has one pole and one zero.  In a typical scope probe, a portion of capacitor C₂ and resistor R₂ are present at the input of the scope itself.  Capacitor C₁ and resistor R₁ are built into the probe and C₁ is tunable.  As the instruction manual guides, you are to apply a square wave to v_in and adjust the capacitor until a square wave is observed on oscilloscope screen. What is this adjustment doing? The presence of C₁ creates a zero in the transmission path.  A pole also exists and is due to all of the capacitance connected at the junction of C₁ and C₂.  The adjustment moves the zero so that it lies on top of the pole thus canceling the effect of both and achieving an infinite bandwidth transmission path!  (We all know you don’t get infinite bandwidth and the reason is because there are other parasitics not accounted for in this simple equivalent model.)  This pole-zero pair that you are aligning by adjusting C₁ is referred to as a pole-zero doublet.

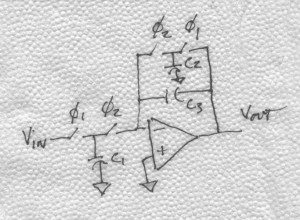
Analog CMOS circuit designers come across pole-zero doublets when trying to maximize  bandwidth of a two-stage operational amplifier without sacrificing stability or settling time.  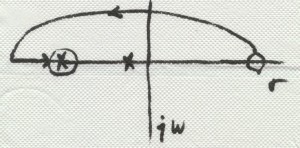The doublet occurs when the you try to move the naturally-occurring right-half-plane zero (due to Miller compensation) into the left-half plane on top of the amplifier’s output load-determined pole as illustrated on BarNapkin 2.

 

You can never get it exactly right. You might think a Bode plot including the effect of the doublet would give you comfort.  Well, it doesn’t–they are close together but you just can’t see their effect in the frequency domain.  However, it is well known that such doublets cause a deterioration of the time-domain response of  the network in which they lie.  Such an effect is often observed to as a “long tail” in the settling response.  How can this be?  Well, if you do the analysis in the time domain (or in the S-domain and dig out your table of Laplace transforms), you will get the answer you are searching for.  For the abstract mind, this is good enough—move on.  But, if you want some intuitive insight, sit back, and enjoy.

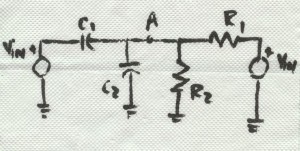
Referring again to BarNapkin 1, the zero comes about from the capacitor C₁ acting with R₁ yielding a zero at w_Z = 1/R₁C₁ and a pole at w_P = 1/(C₂+C₂)(R₁|| R₂).  Applying a simple network-analysis trick allows us to develop some intuition.  Let’s split the input voltage source into two voltage sources—one driving C₁ and the other driving R₁ as illustrated in BarNapkin 3.

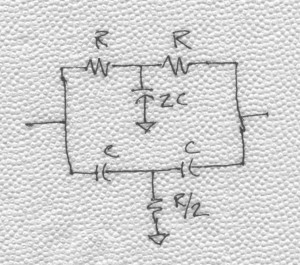
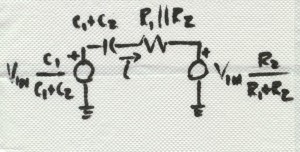
Using Thevenin equivalents looking both ways from node A, we get the equivalent circuit shown on BarNapkin 4.

Nothing has changed about the circuit.  It has been rearranged to aid intuition. Now, with this rearrangement, it is easy to calculate the current flowing through node A.  We can derive the network time constant by examining i(s). We could have stayed in the voltage domain and calculated the voltage across R₁ or R₂. Either way works since the goal is to determine the response to the stimulus, v_in.  The current, i(s), through node A is given as:

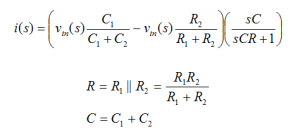
Consider what happens if the two factors of v_in are equal as shown in the following expression.

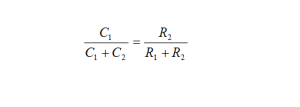
Then

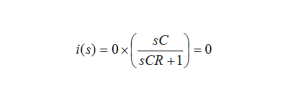
What does zero current mean?  It means that there is no displacement current flowing between the resistors and capacitors.  Thus, the time constant of this circuit appears to be zero or, said another way, the bandwidth appears to be infinity!

Now, if the two factors of v_in are not equal, then the difference forces a current that settles with a time constant of RC as given below

What insight can we glean from these results?  Clearly, placing the pole and zero squarely on top of one another achieves the greatest bandwidth.  However, if they are not coincident, there appears a time constant, t, which settles a voltage difference of

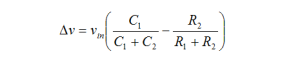
OK, as I said, you could do this analysis in the more classic fashion and arrive at the same understanding (see the expression below for the voltage across R2 resulting from an input step).

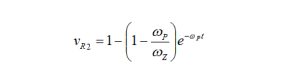
However, applying network simplifications such as the Thevenin equivalent allows for quick insight and can often provide the mathematical insight by inspection.